TP de Synthèse Sonore

Pour ce TP, vous partirez d'un moteur de jeu composé, entre autres, d'un moteur audio minimaliste. L'objectif du TP consiste à écrire différents algorithmes de synthèse sonore, d'un simple bruit blanc jusqu'à un petit synthétiseur granulaire, en ne s'appuyant que sur une librairie vous laissant accès au buffer son (en l'occurence OpenAL).

En premier lieu, il va falloir installer OpenAL. Dans l'archive que je vous donne se trouve l'installeur (engine/utils). Surtout lancez le bien depuis un emplacement local.

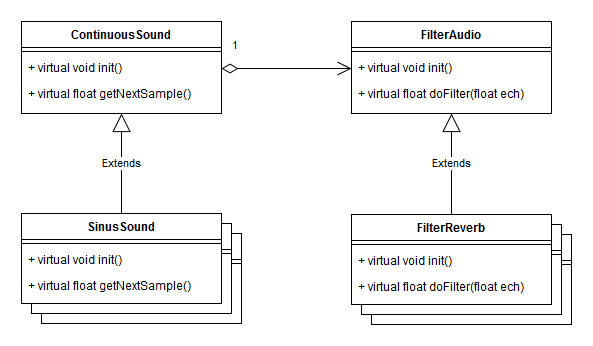
Voici l'architecture du petit moteur son que vous allez modifier. Principalement, le code de la classe ContinuousSound vous donne un buffer tournant et transmet à OpenAL des morceaux de ce buffer régulièrement pour alimenter la carte son. Vos propres classes hériteront de ContinuousSound et de FilterAudio, et vous redéfinirez principalement les méthodes getNextSample() et doFilter().

Attention : par souci de simplicité, le code qui vous est donné fonctionne en 16bits mono. Il peut être facilement modifié pour prendre en compte 8bits ainsi que la stéréo mais en sera d'autant alourdi.

Le TP est construit autour d'une suite d'exercices. Les notions de bases vous serons expliquées au tableau et dans cette page. Vous disposez de la documentation d'OpenAL et d'alut dans la première archive (ci dessous).

Exercice 1 : du blanc au rosé

Complétez la classe NoiseSound pour générer un bruit blanc, en utilisant la fonction randf(). Un bruit blanc produit un son avec une puissance moyenne égale pour toutes les fréquences. Vous remarquerez que par defaut, la classe ContinuousSound génère elle aussi du bruit blanc, vous pouvez vous en inspirer. Oui, ce premier exercice est plutot très simple, pas de piège.

Dans l'interface, cliquez sur Pink Noise pour tester votre son.

Notre objectif va être ensuite de générer un bruit coloré, c'est à dire un bruit pour lequel certaines fréquences sont plus puisssantes que d'autres (ici les graves), et qui aura donc un timbre particulier. Une méthode consisterait à generer un bruit blanc puis à le filtrer pour amoindrir une partie des fréquences, mais pour le moment, nous souhaitons genérer ce son de manière plus directe.

Pour générer un bruit blanc, vous modifiez la valeur du signal à chaque échantillon, vous avez donc un signal qui varie très fréquemment, et donc qui contient des hautes fréquences. Faites varier moins souvent la valeur de l'échantillon, pour obtenir un bruit plus "grave". Vous ajusterez la variabilité de votre variable aléatoire en utilisant l'attribut _FreqNoise, dejà lié au slider correspondant.

Pour obtenir un meilleur résultat, nous allons sommer plusieurs variables aléatoires qui auront chacune leur propre fréquence de variation. Vous utilisez donc le même algorithme que précédement, avec par exemple 8 floats, qui prennent tous une valeur aléatoire, mais dont la valeur varie à des fréquences différentes. Par exemple _FreqNoise pour la première, puis _FreqNoise*2 pour la seconde, etc... Cet algorithme se rapproche de l'algorithme de generation de bruit rose de Voss-McCartney [1] [2]. On remarque que le bruit rose peut êre utilisé pour générer de la musique aléatoire...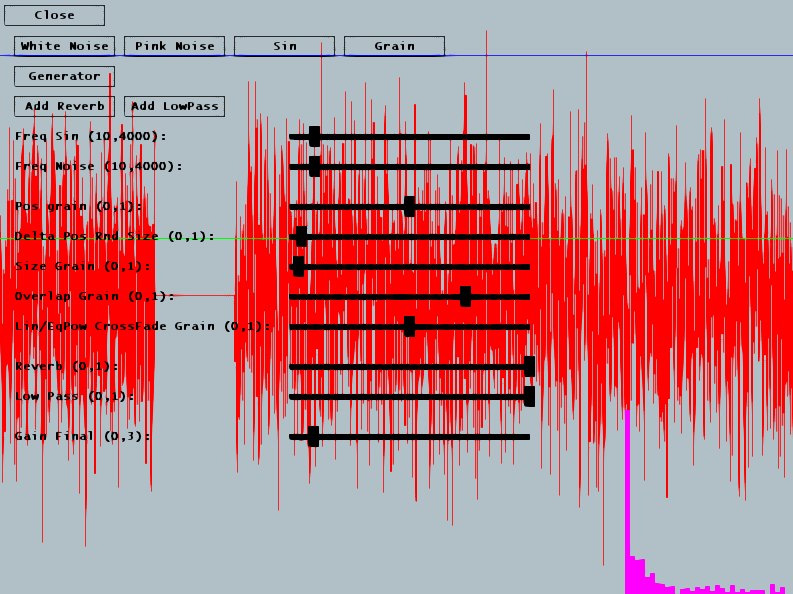

Exercice 2 : Sinusoide

Complétez la classe SinusSound pour générer un son sinusoidal. Sa fréquence soit être celle de _FreqSin. Utilisez pour cela la fonction sin() pour retourner la bonne valeur d'échantillon : un flottant entre -1 et 1, qui sera ensuite ajouté au buffer courant sous forme d'une entier signé 16bits dans ContinuousSound. Attention, -1 et 1 sont les valeur maximales, placez vous plutot entre 0.8 et -0.8 par exemple.

Dans l'interface, cliquez sur Sin pour tester votre son. Le slider freq sin vous permet de modifier la frequence demandée, et se trouve par défaut sur 440Hz. Verifiez que votre son est ok en comparant avec le son d'un sinus 440 (voir youtube par ex).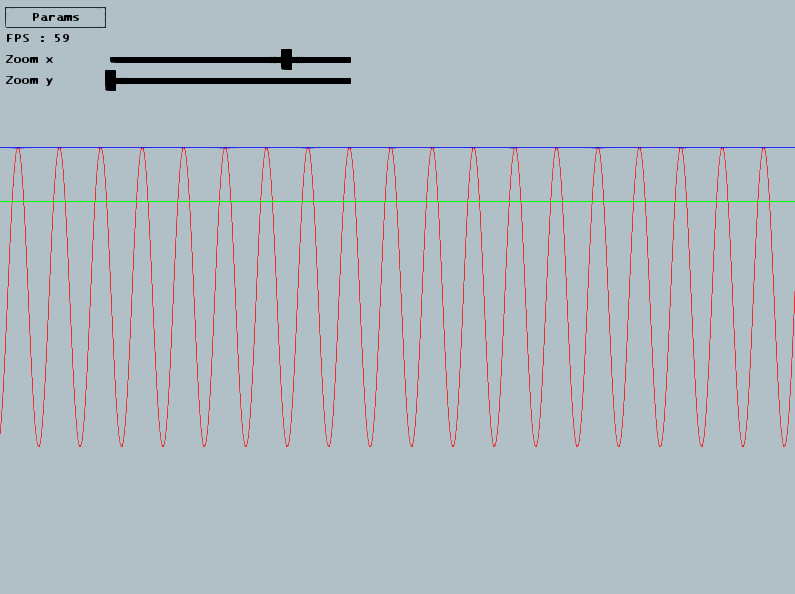

Exercice 3 : Variation de la fréquence

1) Dans votre version actuelle, si on modifie la frequence sur le slider, votre synthé réagit directement ce qui crée une discontinuité. Pour éviter cette discontinuité, réaliser une interpolation plus lente entre la fréquence acutelle du sinus et la fréquence demandée.

2) Comme vous le remarquez, la transition de la fréquence de départ à la fréquence demandée ne se fait pas tout à fait comme on pouvait s'y attendre : c'est un problème de phase. A chaque fois que l'on modifie la fréquence du sinus, on crée une discontinuité dans le signal. Comme on crée cette discontinuité à chaque échantillon, on génère en fait un nouveau signal tout à fait différent, plein de hautes fréquences que nous ne souhaitions pas du tout injécter. Pour régler ce problème, appliquez par exemple la solution suivante :

• 1) Ne modifiez la fréquence du signal qu'à la fin d'une periode, lorsque le signal, qui était jusque la négatif, redevient positif. Cette solution seule n'est pas suffisante car notre signal est échantillonné, et donc impossible de tomber parfaitement à la fin de la période. Mais ca fonctionne déjà mieux.
• 2) Pour que ce soit impeccable, calculez la phase du signal et faites démarrer la période suivante à cette valeur de phase. Bien sur, la periode suivante est générée avec une valeur de fréquence modifiée, pour se rapprocher de la valeur demandée. Pour calculer la phase : on est sur le premier échantillon de notre nouvelle période, donc en $t=0$. On connait la valeur de l'échantillon du début de période (qu'on nommera $g(0)$) puisqu'on veut un signal continu: c'est la valeur qu'aurait eu cet échantillon si on avant pas modifié la fréquence. On cherche donc à sortir $\phi$, la phase, de $g(t) = sin(2\pi f t + \phi)$ avec $t=0$ et $g(0)$ connu... on rappelle que asin() est la réciproque de sin().

Exercice 4 : Filtre Passe Bas

Nous allons maintenant créer un filtre, c'est à dire ici un objet qui va appliquer un traitement sur chaque échantillon produit par un des synthés que vous venez d'écrire (bruit blanc, rose ou sinus). La classe ContinuousSound se charge d'appeler la méthode doFilter() de tout filtre qui lui aura été ajouté. L'interface permet d'ajouter dynamiquement un filtre passe bas et une réverb (qui restent à coder).

Notre premier filtre sera un filtre passe bas. Une manière très simple de coder ce type de filtre consiste à employer la fonction suivante, avec $x(t)$ valeur du signal en entrée du filtre à l'instant $t$ et $y(t)$ valeur du signal en sortie de filtre à l'instant $t$ : $$y(t) = y(t-1) + (\alpha) * (x(t) - y(t-1))$$ On voit que la valeur de sortie du filtre correpond à la valeur de sortie précédente + $\alpha$ fois la distance entre la valeur de sortie précédente et la valeur actuelle du signal. Si $\alpha = 1$ alors on $y(t) = x(t)$ et donc pas de filtrage, et si $\alpha = 0$, on a $y(t) = y(t-1)$, plus rien ne passe, le filtre répète constamment sa sortie précédente. Pour les autres valeurs de $\alpha$, on gomme les différences entre échantillons sucessifs, donc on lisse, donc on élimine les hautes fréquences.

Codez ce filtre en complétant la classe FilterLP. Vous pouvez le tester en cliquant sur Add Low Pass et en modifiant le slider Low Pass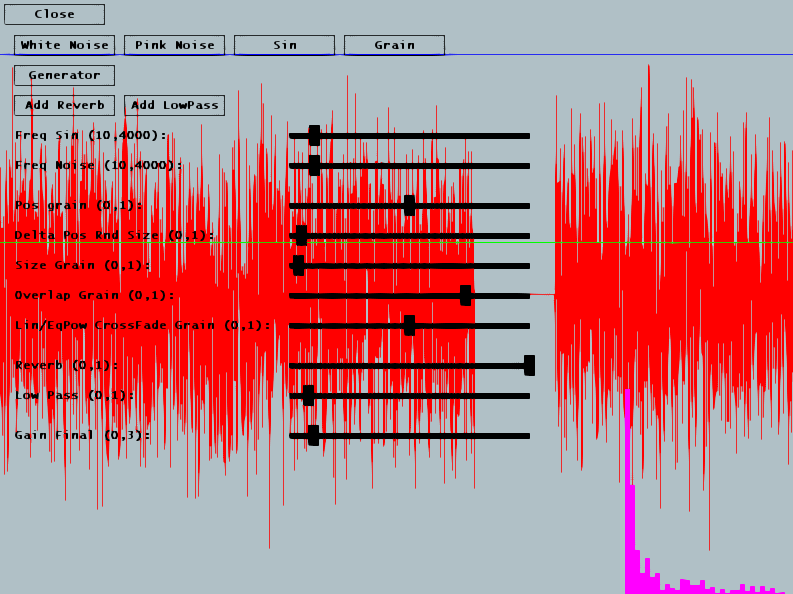

Exercice 5 : Reverb

Comme second filtre, nous allons coder un filtre de réverbération tout simple et faire appel à votre créativité. Le principe de base d'une réverb est le suivant : si la source se trouve dans une zone ouverte, l'écoutant ne perçoit que les ondes sonores qui lui arrivent en ligne directe de la source. Par contre si la zone a une géométrie qui refléchit une partie des ondes sonores en direction de l'écoutant, alors celui ci va percevoir :

• les ondes sonoes provenant directement de la source
• les mêmes ondes sonores issues de la source partant dans une direction autre que celle de l'écoutant, mais renvoyées ensuite par la géométrie dans la direction de l'écoutant.

Les ondes sonore directes et réfléchies sont en partie similaires (tout dépend des propriétés de la surface qui réfléchit les ondes) mais elles ont surtout une différence majeure : elles ne parcourent pas la même distance, et les ondes reflechies sont donc perçues avec un retard. C'est ce mélange avec retard qui crée le phénomène de réverbération.

Le principe de base d'une reverb est donc le suivant : réinjecter dans le signal une partie plus ancienne de ce signal qu'on conserve dans un buffer, comme si elle provenait d'une reflexion. Ce qui caractérise ensuite une réverb par rapport à une autre, c'est le nombre de buffers et la manière dont ils sont agencés.

Les filtres les plus couramment utilisés pour une réverb sont le filtre passe-tout et le filtre en peigne, (all-pass et comb). Comme vous le voyez, ils fonctionnent principalement en ajoutant à l'échantillon en cours un échantillon à $(t-n)$.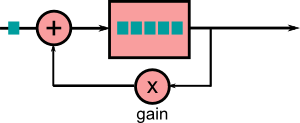

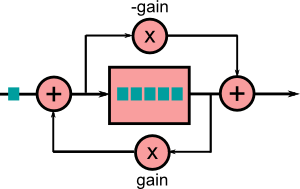
Ces filtres sont ensuite agencés pour crééer une réverb, par exemple en suivant le schéma suivant :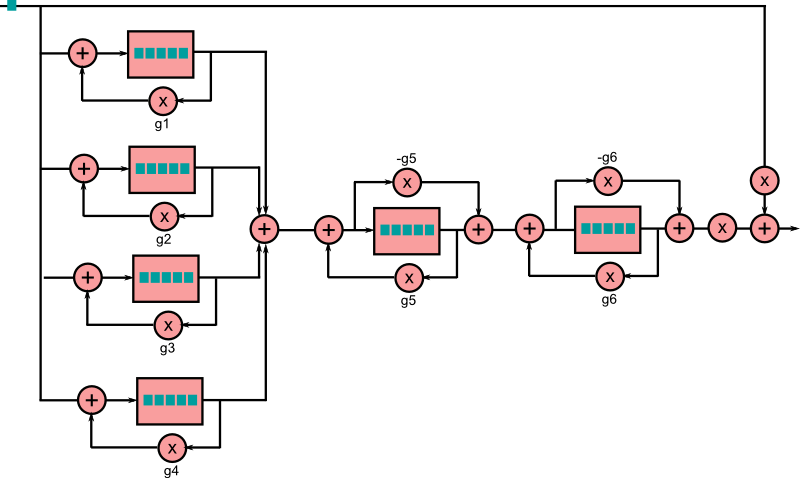

Bien sur, le design d'une reverb est complexe et très variable. Comme nous sommes des programmeurs créatifs, nous pouvons essayer différents arrangements. Par exemple, voici celle que je vous ai mis dans le corrigé. La partie en bleu est répétée $i$ fois. Attention, ce n'est pas l'échantillon directement en sortie qui est récupéré, mais un échantillon dans le buffer de délai. Elle a un rendu bizarre, ce n'est pas une "bonne" reverb. Mais c'est la mienne et elle n'utilise qu'un seul buffer.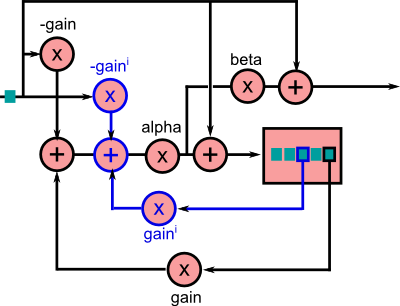

Designez / codez votre propre réverb dans la classe FilterReverb.

Exercice 6 : Synthe Granulaire

Un synthé granulaire est un outil très sympa qui permet de générer un son à partir de fragments d'un fichier audio source, mixés ensemble. Par exemple, avec un fichier son de décollage d'avion, vous pouvez extraire une partie de régime moteur et le répéter à l'infini avec de petites variations, créant ainsi un son de moteur continu. En fait vous pouvez récupérer n'importe quelle texture sonore présente dans un fichier son et l'étirer ainsi à l'infini. Plus les échantillons sont court et plus c'est une texture précise et courte qui est récupérée. De la même manière, avec des échantillons plus longs, vous vous rapprochez plus du fichier d'origine. Vous pouvez par exemple générer une pluie sans fin à partir d'un enregistrement court, sans qu'on percoive de répétition.

La suite de ce TP vous explique comment coder un synthé granulaire.

Synthe Granulaire Step 1 : charger le fichier de base

Vous allez modifier la méthode loadBaseFile(). Vous utiliserez la fonction alutLoadMemoryFromFile() pour charger un fichier wav. Grace aux infos retournés par cette fonction, vous calculerez et afficherez :

• le nombre de pistes du fichier : mono ou stéréo. Les deux voies sont entrelacées.
• le format d'échantillonnage (16b/8b)
• la fréquence d'échantillonnage (nombre d'ech par seconde)
• la taille d'un échantillon en octets
• le nombre total d'échantillons dans le fichier
• la durée totale du fichier en secondes

Vous affichierez ces paramètres sur la console à l'aide de la fonction Log::log(). Alut utilise les defines suivant AL_FORMAT_MONO8, AL_FORMAT_MONO16,AL_FORMAT_STEREO8 et AL_FORMAT_STEREO16 pour le format. Dans ce tp, nous n'utiliserons ensuite que des fichier mono et 16bits pour simplifier le traitement des échantillons (afficher un warning pour les fichiers stereos et 8bits).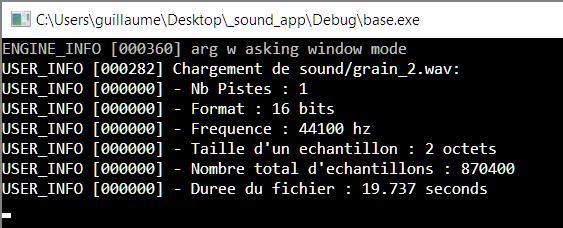

Synthe Granulaire : principe

Il s'agit de sélectionner de très courts fragments du fichier principal, les grains, pour les ajouter ensuite à notre buffer de synthèse. Cette opération s'effectue selon un certain nombre de paramètres, marqués en gras dans la suite du texte.

Extraction de grains depuis le buffer principal

Dans le step 1, vous avez chargé votre fichier son dans un buffer standard en mémoire, représenté par la figure suivante.

De ce buffer, vous allez extraire des grains, c'est à dire des fragments de très courte durée. Attention, il faudra toujours extraire un grain depuis le début d'un échantillon (évident en 8b mono, moins en 16b stéréo). Un grain a une durée donnée, est extrait à partir d'une position donnée, et avec un delta de position aléatoire d'une variabilité donnée. Un grain est donc un simple petit extrait du fichier de base. Il sera ensuite traité avec une attaque et un release, ce qui permet de mixer les grains entre eux : on ne mettra pas les grains les uns à la suite des autres mais on autorisera un certain offset de recouvrement.

Synthe Granulaire Step 2 : créer le buffer de synthèse et effectuer la synthèse

En chargeant le fichier son avec alutLoadMemoryFromFile(), OpenAL vous a alloué un buffer (avec malloc) de la taille du fichier et y a stocké tous les échantillons. De notre côté, nous avons besoin d'un buffer à nous, pour effectuer notre synthèse (écrire et mixer les grains).

A la suite du code précédent, vous allez allouer votre propre buffer de synthèse. Il aura une taille d'environ une seconde. Vous initialiserez également les pointeurs dont vous aurez besoin pour la synthèse : principalement un pointeur d'écriture et un pointeur de lecture.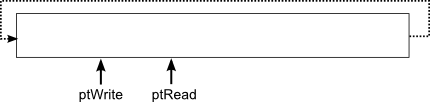

Le principe du buffer tournant est le suivant. Au départ, le pointeur de lecture est à l'échantillon 0, et le pointeur d'écriture à l'échantillon 1. A chaque fois qu'on met à jour le synhté, on va synthétiser des échantillons et les écrire dans le buffer. On commence donc à l'échantillon 1, puis on avance... Une fois arrivé au bout, on reboucle au départ, et on tombe sur le pointeur de lecture : on pause donc la synthèse. En effet, le pointeur de lecture pointe sur le prochain échantillon en attente d'être envoyé à la carte son, qu'on ne souhaite pas écraser.

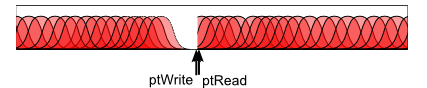
Egalement, on doit transmettre nos échantillons générés à OpenAL. A chaque fois que la fonction getNextSample() va être appelée, c'est que la classe ContinuousSound a justement besoin d'un nouvel échantillon à envoyer à OpenAL. Cette classe envoie des blocs de 100ms à la carte, toutes les 100ms. Donc à chaque appel de getNextSample(), on va retourner l'échantillon placé sous le pointeur de lecture, l'effacer, et avancer le pointeur de lecture. A l'update suivant, on va continuer la synthèse, car le pointeur de lecture aura avancé, et on pourra donc avancer aussi le pointeur d'écriture jusqu'à le rattrapper.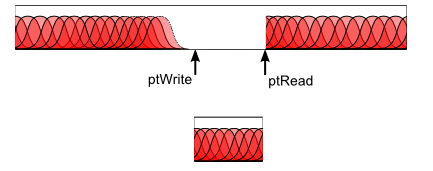

//Declaration d un buffer de 10 octets. 
//Vous pas 10 octets.... mais le nombre d octets necessaires pour 1 seconde de son dans votre format
//On le stoque dans un void * car il peut etre potentiellement 8bits ou 16bits
void * buffer = (void*) new uint8 [10];

//on set le buffer en utilisant un pointeur 16bits si format 16 bits
sint16 * pt = (sint16*) buffer; //Besoin de recaster depuis void *
while(...)
{
	*pt = (sint16)((65535.0f/2.0f) * randf()); //Ici calcul de l echantillon
	pt++; //echantillon suivant
} 

Petite subtilité : si vous mixez les grains avec un cross fade linéaire, c'est à dire $\alpha$ variant linéairement entre 0 et 1 quand on calcule $(1-\alpha) * signal1 + \alpha * signal2$, vous entendrez une perte de puissance au niveau du cross fade. Vous pouvez à la place utiliser un cross fade différent, dit "equal power", par exemple la fonction $\sqrt[2]{t}$, pour le fade in, et $\sqrt[2]{1-t}$ pour le fade out, avec $t \in [0,1]$.

A FAIRE :

• Créer le buffer de synthèse dans la fonction loadBaseFile()
• Mettre à jour le buffer et retourner l'échantillon dans getNextSample()

Rendu

Vous rendrez pour ce TP :

- Les fichiers modifiés
- un executable de votre projet
- une vidéo du soft en train de tourner qui montre les options que vous avez codées (Windows + G)

Bon courage !